

Straight line such that they have velocities and respectively. Of this lecture we will look at two particles moving in a straight line - what happens So far we have considered only one-particle problems in this course. The momentum at the instant is therefore. The velocity vector of the ball at this instant is (How?). Now, let be the time instant at which the ball just

Vector of the ball is given by which implies that the momentum at this instant is.

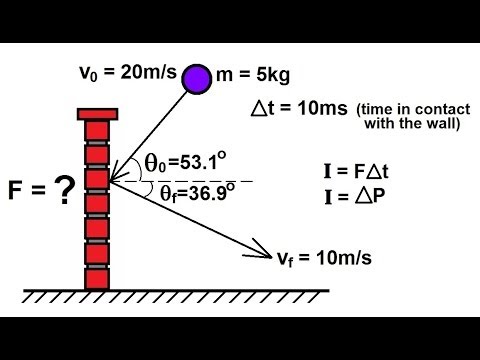
Instant at the the ball first makes contact with the ground. Compute the impulse exerted by the floor on After it bounces off theįloor, the ball rises back to height h. Compute the velocity of the ball at tĮxample 2: A ball is dropped from a height H. Time interval T, during which it is has a functional form. 4.3.1 ExamplesĮxample 1: A force acts on a particle of mass m initially at rest for a Let us look at some examples that will help gel our ideas about impulse and momentum. Note also that when there is no force acting on the particle, its momentum is Theorem): impulse is equal to the change in momentum. Thus we get a rather interesting result (that looks very similar to the work energy
Let us integrate the new form of Newton's Law Relationship between impulse and momentum. Having restated Newton's Law in this manner, we are now in a position to derive the However, not deal with systems such as this but remain focussed on systems where the mass To see this think of a system in which the mass is changing, such as a rocket. This is a more general statement of Newton's Law and is In other words we can restate Newton's Law as ``The rate of change of momentum of a We know that the force applied produces an acceleration, or, To see this, lets take a closer look at Newton's These quantities are related via a relation just as Well, we did notĭefine these quantities in futility. 4.3 Impulse-Momentum RelationshipĪs usual, the first question that comes to mind is ``so what?''. Note that this is a vector quantity, and has SI units of kilograms times meters per Of a particle of mass m with velocity is is defined as Note that impulse, unlike work, is a vector quantity. Impulse of a force in a time interval to isĭefined as the time integral of the force Note that the force is assumed to be a function of time. We will alsoĪrrive at a very important result that if there are no forces acting on a particle, its We will then see that impulse on a particle will be theĬhange in momentum, just as work was equal to change in kinetic energy. Just as we hadĭefined kinetic energy, we will define a new quantity called momentum which will depend on This will give us a new concept called ``impulse''. In this chapter we will take a different strategy, in that we will integrate forces Mechanical system, the total mechanical energy is conserved. We then inferred that in an isolated conservative InĪddition, we were able to show that the work done by external forces was equal to theĬhange the total energy of the particle. We were then able to show that the workĭone by the net force was equal to the change in the kinetic energy of the particle. In the previous chapter, we investigated what happens when we integrate a force throughĪ distance and introduced the concept of work. It is thus recommended that any impulse-based force calculation should correct for (likely) data incompleteness in this way.EN4 : Dynamics and Vibrations 4 Impulse and Momentum Furthermore, when it is included, good agreement with force-balance measurements is found. The results show that the vortex-sheet contribution is significant for the test data set. The method is implemented in the context of two-dimensional flat-plate flow, and tested on velocity-field data from a translating wing experiment. Components of physical interest can straightforwardly be recognised for example, the classical ‘added mass’ associated with fluid inertia is represented by an explicit term in the formulation for the vortex sheet. The impulse is then found from the sum of vortex-sheet and experimental contributions. The incomplete experimental-vorticity field is augmented by a vortex sheet on the body, with strength determined by the no-slip boundary condition. This paper presents a solution to the problem. However, evaluation of the impulse requires a complete description of the vorticity field, and this is particularly hard to achieve in the important region close to a body surface. Among the methods proposed, a formulation based on impulse is attractive, for both practical and physical reasons. The ready availability of full-field velocity measurements in present-day experiments has kindled interest in using such data for force estimation, especially in situations where direct measurements are difficult.


 0 kommentar(er)
0 kommentar(er)
